 |
 |
| Physiology? | Figures & Illustrations | Test Questions | Daily Quiz | Calculators | Physiology Tutor | Glossary |
 |
 |
 |
 |
 |
 |

Monday, December 23, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform volume/volume concentration calculations expressed in parts per trillion (ppt), parts per billion (ppb), parts per million (ppm), parts per thousand (ppth), or parts per hundred (pph, %). The parts-per notation is very common in science and engineering, and is useful when referring to extremely small concentrations. This calculator uses the volume of solute in the numerator and the final volume of solution in the denominator to calculate the concentration (volume/volume fraction). More...
Monday, December 23, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform volume/mass concentration calculations expressed in parts per trillion (ppt), parts per billion (ppb), parts per million (ppm), parts per thousand (ppth), or parts per hundred (pph, %). The parts-per notation is very common in science and engineering, and is useful when referring to extremely small concentrations. This calculator uses the volume of solute in the numerator and the final mass of solution in the denominator to calculate the concentration (volume/mass fraction). More...
Sunday, December 22, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform mass/mass concentration calculations expressed in parts per trillion (ppt), parts per billion (ppb), parts per million (ppm), parts per thousand (ppth), or parts per hundred (pph, %). The parts-per notation is very common in science and engineering, and is useful when referring to extremely small concentrations. This calculator uses the mass of solute in the numerator and the final mass of solution in the denominator to calculate the concentration (mass/mass fraction). More...
Saturday, December 21, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform mass/volume concentration calculations expressed in parts per trillion (ppt), parts per billion (ppb), parts per million (ppm), parts per thousand (ppth), or parts per hundred (pph, %). The parts-per notation is very common in science and engineering, and is useful when referring to extremely small concentrations. This calculator uses the mass of solute in the numerator and the final volume of solution in the denominator to calculate the concentration (mass/volume fraction). More...
Thursday, December 19, 2024
This calculator allows you to determine the number of significant figures for the resulting calculation when two numbers are added, subtracted, multiplied, or divided. The rules of significant figures in mathematical operations are also explained to provide a higher level of learning and understanding. More...
Tuesday, December 17, 2024
This calculator allows you to determine and/or set the significant figures for a number. The rules of significant figures are also explained to provide a higher level of learning and understanding. More...
Monday, December 16, 2024
Scientists must be able to express numbers in a variety of formats including the commonly used scientific notation. In addition, and in particular for experimental scientists, it is imperative that the correct number of significant figures is used when reporting experimentally measured parameters. The calculator below allows you to enter a number in one of three formats (decimal notation, scientific notation, or exponential notation), and will output that number in all three formats. The calculator also determines the number of significant figures for the number provided, or it can use input provided by the user to set the number of significant figures for the number. More...
Thursday, December 12, 2024
Maximum heart rate (HRmax), the highest heart rate that can be achieved with intense physical activity, depends strongly on a person's age. Experimental evidence has shown that HRmax can be estimated by using a simple approximation equation. HRmax ≈ 220 − Age in years. More...
Friday, May 10, 2024
Alveolar minute volume is the volume of inhaled air per unit time (usually per minute) that comes into contact with respiratory exchange surfaces of the lungs (respiratory bronchioles and alveoli). It is the portion of inhaled air that participates in gas exchange. Alveolar minute volume is calculated by multiplying the number of breaths per minute by the difference between tidal volume and dead anatomical space. For an average adult male, alveolar minute volume can be calculated to be 4,200 mL/min, or 12 × (500 − 150). More...
Wednesday, May 8, 2024
Minute volume is the volume of air moved into or out of the lungs per unit time (usually per minute). Therefore, minute volume represents the amount of air inhaled or exhaled per unit time. Minute volume is also referred to as minute ventilation or respiratory minute volume. Minute volume is calculated by multiplying respiratory rate (number of breaths per minute) by the volume of air moved into (inhaled) or out of (exhaled) the lungs per breath (tidal volume). Use this simple calculator to calculate the minute volume. More...
Tuesday, April 23, 2024
Cardiac output refers to the volume of blood pumped by each ventricle of the heart per unit time. Specifically, it is defined as the volume of blood pumped by the left or right ventricle every minute. Cardiac output is calculated by multiplying heart rate (number of heartbeats per minute) by the volume of blood pumped for each heart contraction (stroke volume). Use this simple calculator to calculate the cardiac output. More...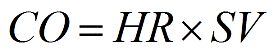
Saturday, April 20, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform calculations for solution mixtures (e.g., mixing two solutions) when working with molal solutions. More...
Saturday, April 20, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform calculations for solution mixtures (e.g., mixing two solutions) when working with normal solutions. More...
Saturday, April 20, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform calculations for solution mixtures (e.g., mixing two solutions) when working with solutions having the following concentration units: parts per billion (ppb), parts per million (ppm), parts per thousand (ppt), and parts per hundred (pph, %). More...
Sunday, April 14, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform calculations for solution mixtures (e.g., mixing two solutions) when working with solutions having units per volume (i.e., units over volume) concentration units such as Units/mL, μUnits/μL, mUnits/mL, Units/L, etc. More...
Sunday, April 14, 2024
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform calculations for solution mixtures (e.g., mixing two solutions) when working with solutions having cells per volume (i.e., cells over volume) concentration units such as cells/mL, cells/L, 103 cells/mL, 106 cells/L, etc. More...
Friday, December 1, 2023
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform calculations for solution mixtures (e.g., mixing two solutions) when working with solutions having mass per volume (i.e., mass over volume) or weight per volume (i.e., weight over volume) concentration units such as pg/mL, μg/μL, mg/mL, g/L, etc. More...
Saturday, November 25, 2023
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform calculations for solution mixtures (e.g., mixing two solutions) when working with molar or percent (%) solutions. More...
Sunday, August 27, 2023
This custom date calculator tool allows you to calculate/generate dates based on a variety of input parameters, such as year, month, weekday, etc. The output can be the date for a single year (1582 to 2500), or dates for a range of years from 1582 to 2500. The calculator uses the Gregorian calendar. More...Monday, August 7, 2023
This simple calculator tool allows you to calculate/generate dates for important holidays, national and international days, and other kay days. The output can be the date for a single year (1582 to 2500). The output can also be the dates for a range of years from 1582 to 2500. The calculator uses the Gregorian calendar. This calculator is especially useful if you wish to know the weekday for a given holiday in a given year (for example, is New Year's Day on a Monday in 2029?). Several common date output formats are available. More...Sunday, February 10, 2019
Meant to be used in both the teaching and research laboratory, this calculator (see below) can be utilized to perform dilution factor calculations when working with solutions having cells per volume (i.e., cells over volume) concentration units such as cells/mL, cells/L, 103 cells/mL, 106 cells/L, etc. More...

Monday, December 31, 2018
Meant to be used in both the teaching and research laboratory, this calculator (see below) can be utilized to perform dilution factor calculations when working with solutions having units per volume (i.e., units over volume) concentration units such as Unit/mL, μUnit/μL, mUnit/mL, Unit/L, etc. More...

Saturday, January 20, 2018
Meant to be used in both the teaching and research laboratory, this calculator (see below) can be utilized to perform dilution factor calculations when working with solutions having mass per volume (i.e., mass over volume) or weight per volume (i.e., weight over volume) concentration units such as pg/mL, μg/μL, mg/mL, g/L, etc. More...

Sunday, January 14, 2018
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution factor calculations when working with solutions having the following concentration units: parts per billion (ppb), parts per million (ppm), parts per thousand (ppt), and parts per hundred (pph, %). More...

Thursday, December 28, 2017
This random password generator allows you to generate very strong and very secure passwords of up to 65,536 characters in length! Several settings allow you to adjust the attributes of the password generated. More...Sunday, December 24, 2017
This random number generator allows you to generate random integers of up to 40 digits. Both positive and negative integers may be generated. More...Saturday, December 23, 2017
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution factor calculations when working with normal solutions. More...

Sunday, December 17, 2017
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution factor calculations when working with molal solutions. More...

Tuesday, December 12, 2017
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution factor calculations when working with molar or percent (%) solutions. More...

Saturday, November 4, 2017
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution factor calculations. More...
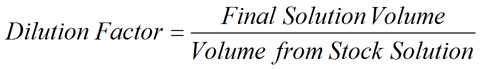
Sunday, April 10, 2016
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform a number of different calculations for preparing normal solutions when starting with the solid material. More...

Saturday, October 17, 2015
The 2015 Nobel Prize in Physiology or Medicine was divided, one half awarded jointly to William C. Campbell and Satoshi Ōmura "for their discoveries concerning a novel therapy against infections caused by roundworm parasites", and the other half awarded to Youyou Tu "for her discoveries concerning a novel therapy against Malaria." Read more from the source at https://www.nobelprize.org/nobel_prizes/medicine/laureates/2015/. More...Sunday, July 26, 2015
Try our unit conversion calculator for converting to and from units commonly used in physiology and other disciplines, as well as units used in everyday life. More...
Wednesday, October 22, 2014
The Hill equation is used to describe substrate-protein interactions that exhibit a sigmoidal shape. The Hill equation is often used to describe the rate of a reaction catalyzed by an enzyme as a function of the substrate concentration. This equation is also commonly used to describe the rate of transporter-mediated translocation of ions and molecules across biological membranes. Examination of reaction kinetics by using the Hill equation is useful because it reveals three important kinetic parameters: (1) the maximum rate of the reaction, also referred to as the maximum reaction velocity (Vmax), (2) the half-maximal concentration constant (K0.5), which is the substrate concentration that gives rise to 50% Vmax, and (3) the Hill coefficient (n), which provides a measure of substrate binding cooperativity. The interactive graph provided in this tutorial allows for a good understanding of the Hill equation, how the reaction velocity changes as a function of the substrate concentration, and how changes in Vmax, K0.5, and n alter the shape of the graph. More...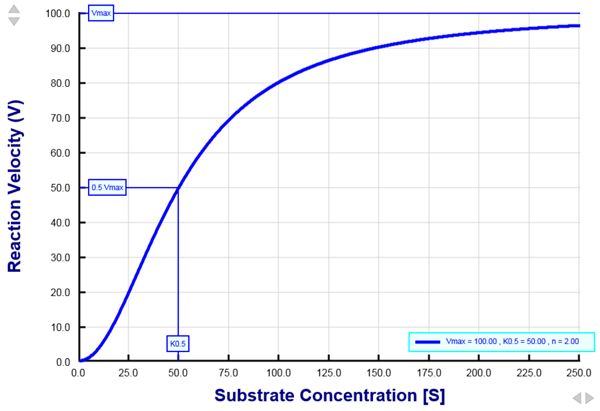
Friday, October 17, 2014
The 2014 Nobel Prize in Physiology or Medicine was divided, one half awarded to John O'Keefe, and the other half awarded jointly to May-Britt Moser and Edvard I. Moser "for their discoveries of cells that constitute a positioning system in the brain." Read more from the source at https://www.nobelprize.org/nobel_prizes/medicine/laureates/2014/. More...Monday, September 1, 2014
The Michaelis-Menten equation is used to describe the rate of a reaction catalyzed by an enzyme as a function of the substrate concentration. This equation is also commonly used to describe the rate of transporter-mediated translocation of ions and molecules across biological membranes. Examination of reaction kinetics by using the Michaelis-Menten equation is useful because it reveals two important kinetic parameters: (1) the maximum rate of the reaction, also referred to as the maximum reaction velocity (Vmax), and (2) the Michaelis constant (Km), which is the substrate concentration that gives rise to 50% Vmax. The interactive graph provided in this tutorial allows for a good understanding of the Michaelis-Menten equation, how the reaction velocity changes as a function of the substrate concentration, and how changes in Vmax and Km alter the shape of the graph. More...
Saturday, February 15, 2014
Cells of multicellular organisms such as animals and plants, as well as those of unicellular organisms such as yeast exhibit a potential difference across the cell plasma membrane. That is to say that there is an electrical potential difference between the inside of the cell and the surrounding bathing medium of the cell. This potential difference is referred to as the membrane potential (Vm). The numerical value of the membrane potential is generally negative, meaning that the inside of the cell is negative with respect to the outside solution, which is taken as the reference or zero value. More...
Wednesday, January 15, 2014
Many professional societies around the world are devoted to the science of physiology. Collectively, these societies and their members continue to advance our understanding of physiological principles at all levels of organization – ranging from molecular physiology to organismal physiology. Physiological societies are also the keepers of physiological knowledge and the history that has led to the current state of knowledge. All physiological societies are committed to providing strong mentorship and training to the next generation of physiologists. More...Sunday, January 5, 2014
In the course measuring physiological parameters, one often needs to make use of one or more fundamental physical constants. The following fundamental physical constants are commonly used in calculations involving physiological parameters. More...Wednesday, October 10, 2012
The 2013 Nobel Prize in Physiology or Medicine has been awarded jointly to James E. Rothman, Randy W. Schekman, and Thomas C. Südhof "for their discoveries of machinery regulating vesicle traffic, a major transport system in our cells". Read more from the source at https://www.nobelprize.org/nobel_prizes/medicine/laureates/2013/. More...Saturday, October 5, 2013
Meant to be used in both the teaching and research laboratory, this calculator (see below) can be utilized to perform a number of different calculations for preparing percent (%) solutions when starting with the solid or liquid material. It is very common to express the concentration of solutions in terms of percentages. Percent means per 100 parts, where for solutions, part refers to a measure of mass (μg, mg, g, kg, etc.) or volume (μL, mL, L, etc.). In percent solutions, the amount (weight or volume) of a solute is expressed as a percentage of the total solution weight or volume. Percent solutions can take the form of weight/volume % (wt/vol % or w/v %), weight/weight % (wt/wt % or w/w %), or volume/volume % (vol/vol % or v/v %). In each case, the percentage concentration is calculated as the fraction of the weight or volume of the solute related to the total weight or volume of the solution. More...


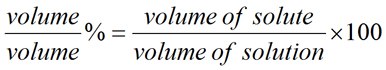
Friday, August 2, 2013
Meant to be used in both the teaching and research laboratory, this calculator (see below) can be utilized to perform a number of different calculations for preparing solutions having mass per volume (i.e., mass over volume) or weight per volume (i.e., weight over volume) concentration units such as mg/mL, μg/μL, μg/L, etc. Such concentration calculations are needed when starting with the solid form of a chemical and a solution needs to be prepared with the concentration unit expressed in unit mass per unit volume (such as mg/mL). These calculations are especially useful when working with compounds that do not have well-defined molecular weights (such as some proteins, carbohydrates, and other polymers). More...
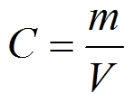
Wednesday, October 10, 2012
The 2012 Nobel Prize in Physiology or Medicine has been awarded jointly to Sir John B. Gurdon and Shinya Yamanaka "for the discovery that mature cells can be reprogrammed to become pluripotent". Read more from the source at https://www.nobelprize.org/nobel_prizes/medicine/laureates/2012/. More...Thursday, July 5, 2012
Neurons rely on a number of mechanisms to perform their important jobs of (i) receiving information, (ii) information processing, (iii) signal propagation, and (iv) signal transmission. One such mechanism that is at the core of neuronal function is based on rapid and reversible reversal of the electrical potential difference across the plasma membrane. By reversal, it is meant that the membrane potential rapidly changes from its resting level of approximately −70 mV to around +50 mV and, subsequently, rapidly returns to the resting level again. The rapid reversal of membrane potential forms an important basis for information processing, propagation, and transmission and is referred to as the action potential, electrical impulse, or nervous impulse. In this fashion, neurons are said to be excitable cells. The focus of this lecture is to learn about the details of the neuronal action potential. Neurons are not the only excitable cells in the human body. Muscle cells (skeletal, cardiac, and smooth muscle), and some endocrine cells (i.e., hormone producing cells) are also excitable (i.e., exhibit action potentials). These cells will be discussed in later lectures. More...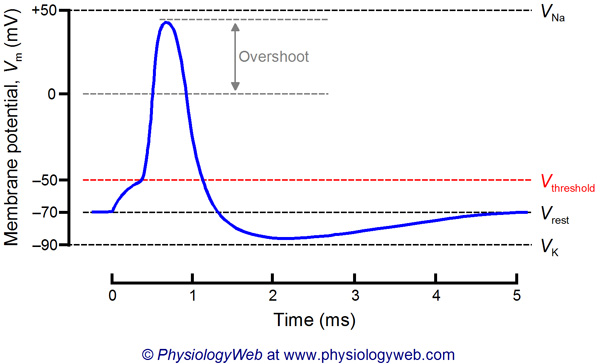
Thursday, December 1, 2011
The 2011 Nobel Prize in Physiology or Medicine has been divided, one half jointly to Bruce A. Beutler and Jules A. Hoffmann "for their discoveries concerning the activation of innate immunity" and the other half to Ralph M. Steinman "for his discovery of the dendritic cell and its role in adaptive immunity". Read more from the source at https://www.nobelprize.org/nobel_prizes/medicine/laureates/2011/. More...Monday, July 4, 2011
When two or more ions contribute to the membrane potential across the plasma membrane (Vm) of a cell, it is likely that the membrane potential would not be at the equilibrium potential (Veq.) for any of the contributing ions. Thus, no ion would be at its equilibrium (i.e., Veq. ≠ Vm). When an ion is not at its equilibrium, an electrochemical driving force (VDF) acts on the ion, causing the net movement of the ion across the membrane down its electrochemical gradient. The driving force is quantified by the difference between the membrane potential and the ion equilibrium potential (VDF = Vm − Veq.). The magnitude of the driving force indicates how far an ion is from its electrochemical equilibrium. The arithmetic sign (i.e., positive or negative) of the driving force acting on an ion along with the knowledge of the valence of the ion (i.e., cation or anion) can be used to predict the direction of ion flow across the plasma membrane (i.e., into or out of the cell). More...
Sunday, June 12, 2011
The Nernst equation describes the electrochemical equilibrium distribution of an ion between two compartments that are separated by a membrane that contains channels selective for that ion. In an ideal case, the membrane separating the two compartments allows only the passage of the ion of interest and no other ion. The distribution of the ion across the membrane is governed by the ion concentration gradient across the membrane and leads to the establishment of a potential difference across the membrane. At equilibrium, this potential difference is described by the Nernst equation, and is referred to as the equilibrium potential (Veq.) or Nernst potential for that ion. The Nernst equation can be derived based on simple thermodynamic principles. More...
Sunday, May 29, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform a number of different calculations for preparing solutions having units per volume (i.e., units over volume) concentration units such as Units/mL, μUnits/μL, mUnits/mL, Units/L, etc. Such concentration calculations are needed when starting with the solid form of an enzyme (such as collagenase), haparin, or any other biologically active molecule, where the activity unit is noted in Units/mg, and a solution needs to be prepared with the concentration unit expressed in activity unit per unit volume such as Units/mL. More...

Friday, May 20, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform a number of different calculations for preparing molal solutions when starting with the solid material. More...

Monday, May 16, 2011
The International System of Units (SI) prefixes are conveniently used to express fractions or multiples of any given unit, and are particularly useful when working with very large or very small numbers. For example, 100 kilometers (km) can be used instead of 100,000 meters (m). As another example, it is more convenient to state that the diameter of a typical mammalian cell is approximately 10 μm rather than 0.00001 m (or 10 × 10-6 m). More...Friday, May 13, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution calculations when working with solutions having cells per volume (i.e., cells over volume) concentration units such as cells/mL, cells/L, 103 cells/mL, 106 cells/L, etc. These calculations are commonly performed when working with culture media containing living cells such as bacterial cells or mammalian cells. More...
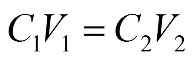
Monday, May 2, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution calculations when working with solutions having units per volume (i.e., units over volume) concentration units such as Units/mL, μUnits/μL, mUnits/mL, Units/L, etc. More...
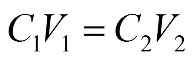
Saturday, April 23, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution calculations when working with solutions having mass per volume (i.e., mass over volume) or weight per volume (i.e., weight over volume) concentration units such as pg/mL, μg/μL, mg/mL, g/L, etc. More...
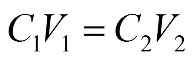
Wednesday, April 20, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution calculations when working with solutions having the following concentration units: parts per billion (ppb), parts per million (ppm), parts per thousand (ppt), and parts per hundred (pph, %). More...
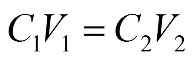
Wednesday, April 20, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution calculations when working with normal solutions. More...
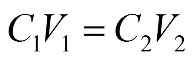
Tuesday, April 19, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution calculations when working with molal solutions. More...
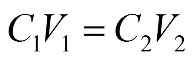
Sunday, April 17, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform dilution calculations when working with molar or percent (%) solutions. More...
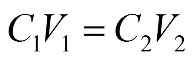
Wednesday, April 13, 2011
Meant to be used in both the teaching and research laboratory, this calculator can be utilized to perform a number of different calculations for preparing molar solutions when starting with the solid material. More...

Saturday, April 9, 2011
Physiology is the study of how living systems function. Scientists who study physiology are called physiologists. Physiologists attempt to describe biological phenomena in physical and chemical terms. Physiologists come to the field with extremely diverse backgrounds and apply their specialized skills and knowledge to understanding the function of living systems. Physiologists study living systems from the subcellular level (molecules and organelles) all the way to the level of the whole organism and how organisms adapt to vastly different environmental conditions such as hot, cold, dry, humid, or high altitude. In their attempt to elucidate the mechanisms operating in living systems, physiologists make use of an enormous array of experimental techniques. Techniques of cell and molecular biology, genetics, genomics, bioinformatics, chemistry, physics, and engineering, all find applications in the study of living systems by physiologists. More...
Sunday, March 27, 2011
When considering the diffusion of ions and molecules in solutions, it is generally useful to be able to estimate the time required for diffusion over a given distance. From a physiological perspective, this knowledge helps us better understand how long it takes molecules and ions to travel physiologically relevant distances by diffusion alone. For example, it is of value to know how long it takes molecular O2 to reach metabolically active cells 10 μm away from a capillary. As another example, it is important to know how long it takes a neurotransmitter molecule released from the pre-synaptic neuron to diffuse across the synaptic cleft of 20-50 nm to reach target receptors on the post-synaptic plasma membrane. Likewise, numerous other physiological examples can be considered. While in solutions, diffusing solutes move in three dimensions down a concentration gradient from an area of higher concentration to an area of lower concentration, a simple equation may be used to approximate the time it takes a given molecule to diffuse an average distance in one dimension (see equation below). This calculator allows you to calculate the time it takes for a solute to diffuse a given distance in one direction along one axis. More...
Saturday, March 19, 2011
The mean arterial pressure (MAP) is the force that drives blood through the vasculature from the arteries to arterioles, capillaries, venules, veins, and back to the heart. The mean arterial pressure is a time-weighted average of pressure values in large systemic arteries during the cardiac cycle. The mean arterial pressure is a function of (1) the rate at which the heart pumps blood into the large arteries, (2) the rate of blood flow out of the large arteries to enter smaller arteries and arterioles, and (3) arterial wall compliance. If the ventricles spent an equal length of time in systole and diastole, the mean arterial pressure could simply be estimated as the mathematical average of systolic and diastolic pressure values. In reality, however, the ventricles spend approximately one-third (1/3) of their time in systole, and two-thirds (2/3) in diastole (see figure below). Therefore, a simple average of the systolic and diastolic pressure values is not an acceptable estimate of the mean arterial pressure. Instead, a simple approximation equation is typically used to estimate the mean arterial pressure, where mean arterial pressure = diastolic pressure + (1/3) × pulse pressure. Pulse pressure is the difference between systolic and diastolic pressure values. This calculator allows you to calculate the mean arterial pressure based on known systolic and diastolic pressure values. More...
Monday, March 14, 2011
The temperature coefficient (Q10) represents the factor by which the rate (R) of a reaction increases for every 10-degree rise in the temperature (T). The rate (R) may represent any measure of the progress of a process. For example, the rate may be the velocity of action potential propagation along a nerve fiber (e.g., m/s), or it may be the rate at which the products of a chemical reaction are produced (e.g., mmol/s), or it may be the current (electrical equivalent of ionic flux) conducted through an ion channel, pump, or transporter (e.g., pA, nA, µA, etc.), or it may be the rate at which the heart contracts per minute (i.e., beats per minute, bpm). Q10 values are useful because they may be used to infer mechanistic insight about the physiological process under investigation. This calculator allows you to calculate the Q10 for a chemical reaction or a physiological process. More...Saturday, February 19, 2011
In living cells, the resting membrane potential (Vm) is seldom governed by only one ion such as K+, Na+, Cl-, etc. If this were the case, the membrane potential could be predicted by the equilibrium potential (VEq.) for that ion, and could be easily calculated by using the Nernst equation. Instead, the membrane potential is generally established as a result of the relative contributions of several ions. In many cells, K+, Na+, and Cl- are the main contributors to the membrane potential. For example, in a typical mammalian neuron, K+, Na+, and Cl- contribute to a resting membrane potential of around -70 mV, a membrane potential value that is not at the equilibrium potential for K+, Na+, or Cl-. This is because in neurons at rest, there are K+-, Na+- and Cl--selective channels in the plasma membrane. These selective ion channels allow K+, Na+, and Cl- to each move down its own electrochemical gradient. The movement of any ion down its own electrochemical gradient will tend to move the membrane potential toward the equilibrium potential for that ion. Therefore, the transmembrane movements of all three ions (K+, Na+, and Cl-) collectively contribute to the membrane potential. When more than one ion channel is present (and open) in the plasma membrane, the membrane potential can be calculated by using the Goldman-Hodgkin-Katz equation (GHK equation). More...Wednesday, February 16, 2011
The Nernst equation calculates the equilibrium potential (also referred to as the Nernst potential) for an ion based on the charge on the ion (i.e., its valence) and its concentration gradient across the membrane. Temperature also influences the Nernst potential (see Nernst equation below). A Nernst potential will develop across a membrane if two criteria are met: (1) if a concentration gradient exists across the membrane for a given ion, and (2) if selective permeation pathways (i.e., selective ion channels) exist that allow transmembrane movement of the ion of interest. More...Sunday, February 13, 2011
The body mass index (BMI) was developed in the mid nineteenth century (~1850s) by the Belgian Adolphe Quetelet in an effort to identify a simple screening parameter for reporting one's weight as a function of his/her height. BMI is used as an indicator of body fat content and, based on established threshold values, it provides a quantifiable index of one's health status and risk factors with respect to body weight. This calculator allows you to determine your own BMI. More...Thursday, February 10, 2011
Secondary active transport is a form of active transport across a biological membrane in which a transporter protein couples the movement of an ion (typically Na+ or H+) down its electrochemical gradient to the uphill movement of another molecule or ion against a concentration/electrochemical gradient. Thus, energy stored in the electrochemical gradient of an ion is used to drive the transport of another solute against a concentration or electrochemical gradient. The ion moving down its electrochemical gradient is referred to as the driving ion because it is movement of this ion that drives the uphill movement of another ion/molecule (driven ion/molecule). Secondary active transport is also commonly referred to as ion-coupled transport and, in fact, coupling between the driving and driven species is obligatory. More...
Monday, January 24, 2011
Facilitated diffusion (also known as facilitated transport) is a form of passive transport across a biological membrane in which a transporter protein facilitates (or mediates or catalyzes) the movement of an otherwise membrane-impermeant molecule or ion across the plasma membrane down its concentration or electrochemical gradient. The transport proteins responsible for this function are referred to as facilitative transporters or uniporters, examples of which include the ubiquitous glucose transporters (GLUT family), a variety of amino acid transporters, and others. Collectively, these transporters perform many essential cellular and organismal functions. In facilitated diffusion, the direction of transport is always down a concentration gradient from one side of the membrane where the substrate concentration is high to the other side of the membrane where the concentration is lower. The cartoon shown below is a simplified conceptual representation of the workings of a typical facilitative transporter. More...Friday, January 21, 2011
Other than lipid-soluble molecules (steroids, O2, CO2, etc.) and some very small polar molecules (water, urea, ethanol, glycerol) (see Lipid Bilayer Permeability), the passage of ions and most polar molecules across biological membranes requires the presence of integral membrane proteins that function as transport proteins. Transport proteins are referred to as transporters or, less commonly, carriers, and may be active transporters or passive transporters. The figure shown below summarizes the major pathways by which molecules/ions can cross biological membranes. More...
Monday, January 17, 2011
All living cells must be able to exchange materials (nutrients and waste products) with their external environments in order to remain alive. Because the phospholipid bilayer is responsible for forming membranes and hence compartments, it is important to understand how various molecules can pass through this lipid bilayer. Simply stated, biological membranes are semipermeable lipid bilayers. Permeability refers to the ease with which molecules cross biological membranes. More...
Neuronal Action Potential
Tuesday, October 12, 2010
Excitable cells of the nervous system (i.e., neurons) generate nervous impulses. Nervous impulses are the electrical signals by which neurons talk to one another and also to other cells of the body. The nervous impulse is referred to as the action potential. An action potential is a brief (only a few milliseconds) reversal of the membrane potential (Vm). At rest, the Vm of a neuron is around -70 mV (close to the equilibrium potential for potassium, VK), but during an action potential, Vm transiently approaches +50 mV (close to the equilibrium potential for sodium, VNa). The membrane potential then rapidly returns to the resting potential and even briefly goes beyond the resting potential to approach VK before finally returning to the resting value of about –70 mV. The entire process takes about 3–5 ms. This potential reversal of more than 100 mV is responsible for electrical signaling in the nervous system, and is the basis of information transmission in the nervous system.
Test your basic knowledge of the neuronal action potential by taking this simple quiz. For more information about the neuronal action potential, see the Neuronal Action Potential lacture notes.
Water Reabsorption by The Kidneys
Monday, October 11, 2010
Did you know that the kidneys of an average adult human being filter about 180 L of plasma every day! That is every day, the entire volume of plasma is filtered about 50 times by the kidneys! This massive amount of filtration is indeed necessary to allow the kidneys to eliminate waste products present in the plasma. Most of these waste materials are the byproducts of normal metabolism. They are removed from the plasma through filtration (and secretion for some) in the kidneys and ultimately are eliminated from the body through urine. However, a significant amount (in fact most) of the filtered water must be reabsorbed in order to prevent life-threatening dehydration.
Test your basic knowledge of kidney filtration and reabsorption by taking this simple quiz.
Past Recipients of the Nobel Prize in Physiology or Medicine
Friday, October 8, 2010
The Nobel Prize bestows upon a scientist the highest scientific honor possible. While most scientists pursue their intellectual passion without ever expecting to achieve fame, becoming a Nobel Prize recipient is the closest thing to "rock star" status for a scientist. Yet, it is often noted that many scientists have a limited knowledge of the history of the prize even in their own discipline. Test your knowledge of the past recipients of the Nobel Prize in Physiology or Medicine by taking this simple quiz.2010 Nobel Prize in Physiology or Medicine
Monday, October 4, 2010
The 2010 Nobel Prize in Physiology or Medicine has been awarded to Robert G. Edwards for pioneering work in reproductive physiology and, particularly, for developing the in-vitro fertilization (IVF) procedure in 1977, which was revealed to the world by the birth of the first ever "test-tube baby" on July 25, 1978. As of this writing, the procedure is estimated to have led to the birth of about 4 million children. Read more from the source at https://nobelprize.org/.
Posted: Thursday, September 16, 2010
Last updated: Sunday, December 22, 2024
Last updated: Sunday, December 22, 2024