 |
 |
| Physiology? | Figures & Illustrations | Test Questions | Daily Quiz | Calculators | Physiology Tutor | Glossary |
 |
 |
 |
 |
 |
 |

Resting Membrane Potential -
Nernst Equilibrium Potential
Nernst Equilibrium Potential
In the previous section of this lecture (Establishment of the Membrane Potential), we learned the two requirements for establishing a membrane potential: (1) ion concentration gradient across the membrane, and (2) selective ion channels in the membrane. We learned that the concentration gradient (i.e., chemical gradient) causes the ion to move from the compartment with the higher ion concentration to the compartment with the lower ion concentration. We learned that the movement of an ion across the membrane that is not balanced by the movement of a counter ion leads to charge separation across the membrane, and that this charge separation forms the basis for the establishment of a potential difference across the plasma membrane (i.e., membrane potential, Vm). Charge separation across the membrane leads to the establishment of an electrical gradient that grows in magnitude until it exactly balances the chemical gradient. When the chemical and electrical gradients are equal in magnitude, the ion is said to be in electrochemical equilibrium, and the membrane potential that is established at equilibrium is said to be the equilibrium potential (Veq.) for that ion under the existing concentration gradient.
Now letís examine the chemical and electrical gradients more closely so that we can gain a quantitative understanding of these two forces that act on ions. Our ultimate goal is to arrive at an equation that will allow us to calculate the value of the equilibrium potential based on the nature of ion (i.e., valence of the ion), as well as the ion concentration gradient that exists across the membrane. Here, we take a simplified approach to deriving this equation. A more rigorous approach is discussed under Derivation of the Nernst Equation. We will use K+ for this derivation and will later extend the equation to other ions. We begin by determining the free energy (ΔG) available from the chemical and electrical gradients. The chemical gradient (ΔGChemical) and the electrical gradient (ΔGElectrical) can be defined as:
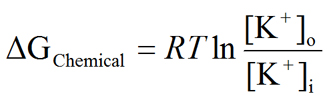 |
Eq. 1 |
and
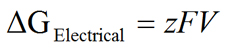 |
Eq. 2 |
where R is the gas constant, T is the absolute temperature, F is the Faraday constant, V is the voltage, and z is the valence of K+ (+1). At equilibrium, ΔGElectrical and ΔGChemical are equal. Therefore,
 |
Eq. 3 |
Substituting for ΔGChemical and ΔGElectrical, we get
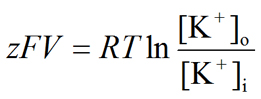 |
Eq. 4 |
Solving for V, we get
 |
Eq. 5 |
The above equation (Eq. 5) is known as the Nernst equation. The Nernst equation allows us to calculate the potential that will be established across the membrane based on the valence and concentration gradient of K+ (provided that only K+ channels are present). This potential is also referred to as the Nernst potential. The Nernst potential for any given ionic species is the membrane potential at which the ionic species is in equilibrium; i.e., there is no net movement of the ion across the membrane. Therefore, the Nernst potential for an ion is referred to as the equilibrium potential (Veq.) for that ion. At the equilibrium potential, the chemical and electrical gradients are equal and opposite in direction. For example, the Nernst potential for K+ is the equilibrium potential for K+ (VK). The generalized form of the Nernst equation is:
 |
Eq. 6 |
where,
- Veq. is the equilibrium potential (Nernst potential) for a given ion. It is common to use the ion symbol as a subscript to denote the equilibrium potential for that ion (e.g., VK, VNa, VCl, VCa, etc.). If only one ionic species is present in the system and channels for only the ionic species are present (and open), then Veq. will also be the membrane potential (Vm). Note that the unit of Veq. is the Volt. However, the equilibrium potential is typically reported in millivolts (mV).
- R is the universal gas constant and is equal to 8.314 J.K−1.mol−1 (Joules per Kelvin per mole).
- T is the temperature in Kelvin (K = °C + 273.15).
- z is the valence of the ionic species. For example, z is +1 for Na+, +1 for K+, +2 for Ca2+, −1 for Cl−, etc. Note that z is unitless.
- F is the Faraday's constant and is equal to 96,485 C.mol−1 (Coulombs per mole).
- [X]out is the concentration of the ionic species X in the extracellular fluid. Note that the concentration unit must match that of [X]in.
- [X]in is the concentration of the ionic species X in the intracellular fluid. Note that the concentration unit must match that of [X]out. Typically, but not always, the concentrations are noted in mM.
- The Nernst equation can be derived based on simple thermodynamic principles (see Derivation of the Nernst Equation).
- The Nernst potential calculator may be used not only to perform calculations, but also to gain a good understanding of this equation.
- If two or more ions contribute to the membrane potential, the Nernst potential no longer yields the Vm. In this case, use the Goldman-Hodgkin-Katz (GHK) equation to calculate the Vm.
We should examine the Nernst equation closely in order to gain an intuitive understanding for the Nernst potential. First, it is reiterated here that for the Nernst potential to be established, selective channels must be present and open. Second, by examining the Nernst equation, it becomes immediately obvious that only three factors are important in determining the magnitude and direction of the Nernst potential. These three factors are (1) the concentration gradients, (2) the valence of the ionic species in question, and (3) temperature. If there is no concentration gradient across the plasma membrane, the ratio of the extracellular to intracellular concentration terms becomes 1. The natural logarithm of 1 is zero. Hence, there will be no potential difference across this membrane, even if the channels for the ion were fully open. Therefore, a concentration difference is essential in establishing a Nernst potential. The valence of the ion also influences the magnitude and direction of the Nernst potential for the ion. Note that the Nernst potential varies indirectly with the ionic valence. Temperature (T) also plays a small role in determining the magnitude of the Nernst potential. A few examples are presented below to show how the Nernst equation is used to determine the equilibrium potential for various ions.
If the ion in question is K+, the Nernst equilibrium potential for K+ (VK) will be:
 |
Eq. 7 |
If the ion in question is Na+, the Nernst equilibrium potential for Na+ (VNa) will be:
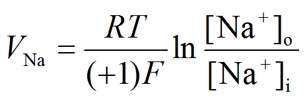 |
Eq. 8 |
If the ion in question is Ca+, the Nernst equilibrium potential for Ca2+ (VCa) will be:
 |
Eq. 9 |
If the ion in question is H+ (hydrogen ion or proton), the Nernst equilibrium potential for H+ (VH) will be:
 |
Eq. 10 |
If the ion in question is Cl−, the Nernst equilibrium potential for Cl− (VCl) will be:
 |
Eq. 11 |
If the ion in question is HCO3− (bicarbonate), the Nernst equilibrium potential for HCO3− (VHCO3−) will be:
 |
Eq. 12 |
If the ion in question is SO42−, the Nernst equilibrium potential for SO42− (VSO4−−) will be:
 |
Eq. 13 |
and so on.
For a typical mammalian cell in its natural environment (37 °C), the following ionic equilibrium potentials can be calculated. The Nernst Potential Calculator can be used to perform these calculations.
Table 1. Intracellular and extracellular concentrations and Nernst equilibrium potential values for a few ions of physiological importance
| Ionic Species | Intracellular Concentration | Extracellular Concentration | Equilibrium Potential |
| Sodium (Na+) | 15 mM | 145 mM | VNa = +60.60 mV |
| Potassium (K+) | 150 mM | 4 mM | VK = −96.81 mV |
| Calcium (Ca2+) | 70 nM | 2 mM | VCa = +137.04 mV |
| Hydrogen ion (proton, H+) | 63 nM (pH 7.2) | 40 nM (pH 7.4) | VH = −12.13 mV |
| Magnesium (Mg2+) | 0.5 mM | 1 mM | VMg = +9.26 mV |
| Chloride (Cl−) | 10 mM | 110 mM | VCl = −64.05 mV |
| Bicarbonate (HCO3−) | 15 mM | 24 mM | VHCO3- = −12.55 mV |
If there are only K+ channels in a cell, then Vm in this cell will be the same as the K+ equilibrium potential (VK) which can be obtained from the Nernst potential for K+. Therefore, in this cell, Vm = Vrest = VK, which is what you expect because K+ distributes itself across the membrane according to the Nernst equation which describes the situation at equilibrium (of course, the K+ channels have to be open to allow K+ to redistribute itself across the membrane according to the chemical and electrical potential gradients). At VK, there is no net movement of K+ across the membrane. Similarly, if there are only Na+ channels in the cell (and are open), at equilibrium, Vm = Vrest = VNa. If there are only Cl− channels in the cell (and are open), at equilibrium, Vm = Vrest = VCl.
If there are more than one type of channels that are open at any given time, the situation is slightly more complex (see next section for details). Now the resting potential can no longer be described as an equilibrium potential because no ion is at equilibrium (Vm = Vrest ≠ Veq.). This is because many ions are contributing to the resting potential, and the final value of the resting potential will depend on the concentration gradients and the relative membrane permeabilities of the ions in the system. When multiple ions are present, each ion is moving down its own electrochemical potential gradient. In this case, the system is said to be at steady-state. Although there are exceptions, in most mammalian cells, the major ions contributing to Vrest are K+, Na+, and Cl−. In the next section, we will describe how different ions contribute to the membrane potential in real cells.
Posted: Saturday, February 15, 2014